8-14 698 views
作者:nenn(百度id:正正正正正好)
注1:本文中提到的所有Minecraft版本均为1.12。
注2:相关数学推导需要高等数学知识(大学理工科专业一年级内容),涉及求导、微分和积分的计算。
1.水平动力直轨(I类铁轨)上矿车运动的数学模型
目前为止,通过[1]和[2]中对动力直轨(I类铁轨)的研究,我们已经获得了较为成熟的数学模型。这一模型表述如下:
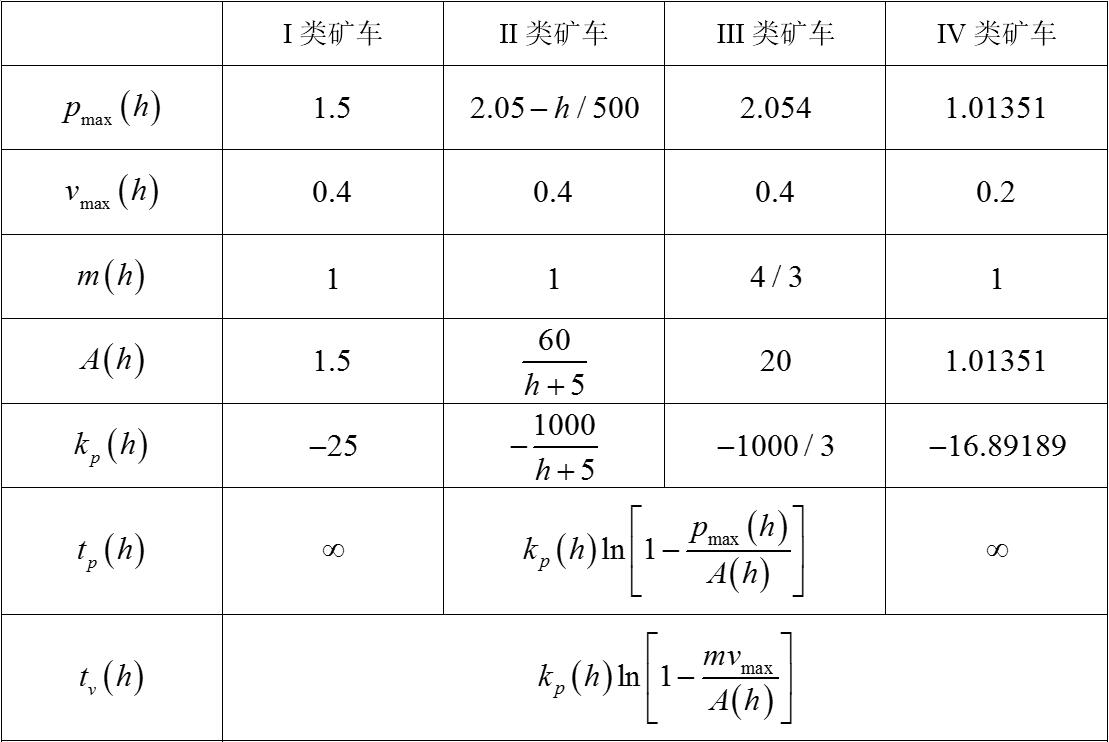

通过Matlab编程,可以很容易地验证其正确性:
红、蓝、绿、粉分别代表I、II、III和IV类矿车。
t 为耗时,m* 为矿车的有效质量,p 为矿车的动量,F 为I类铁轨对矿车的作用力,S 为滑行距离,v 为矿车速度,a 为矿车加速度。
可见,其结果与[1]中展示的实验数据相吻合。
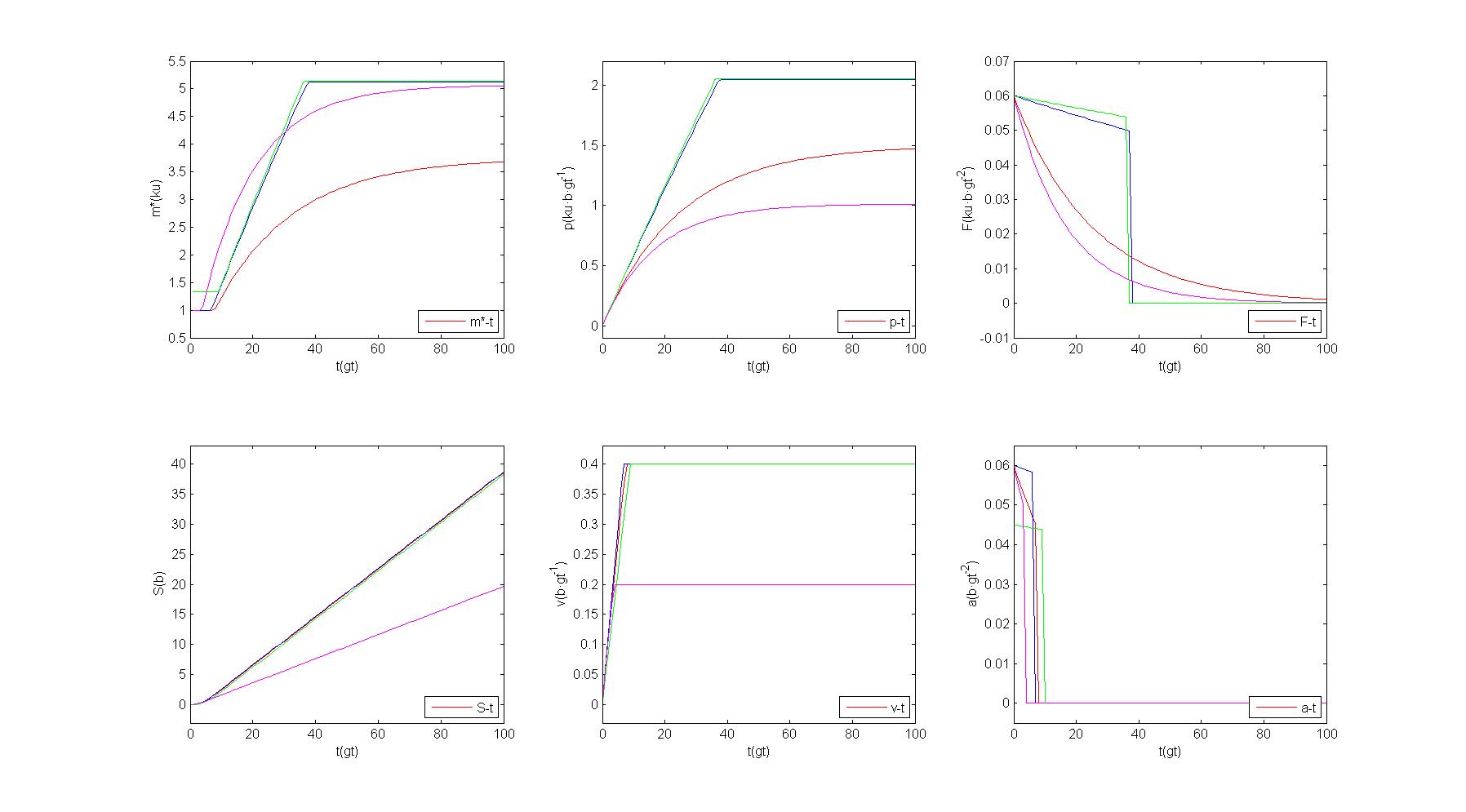
红、蓝、绿、粉四色循环分别代表不同载物量的II类矿车。
t 为耗时,m* 为矿车的有效质量,p 为矿车的动量,F 为I类铁轨对矿车的作用力,S 为滑行距离,v 为矿车速度,a 为矿车加速度。
可见,其结果与[2]中展示的实验数据相吻合。
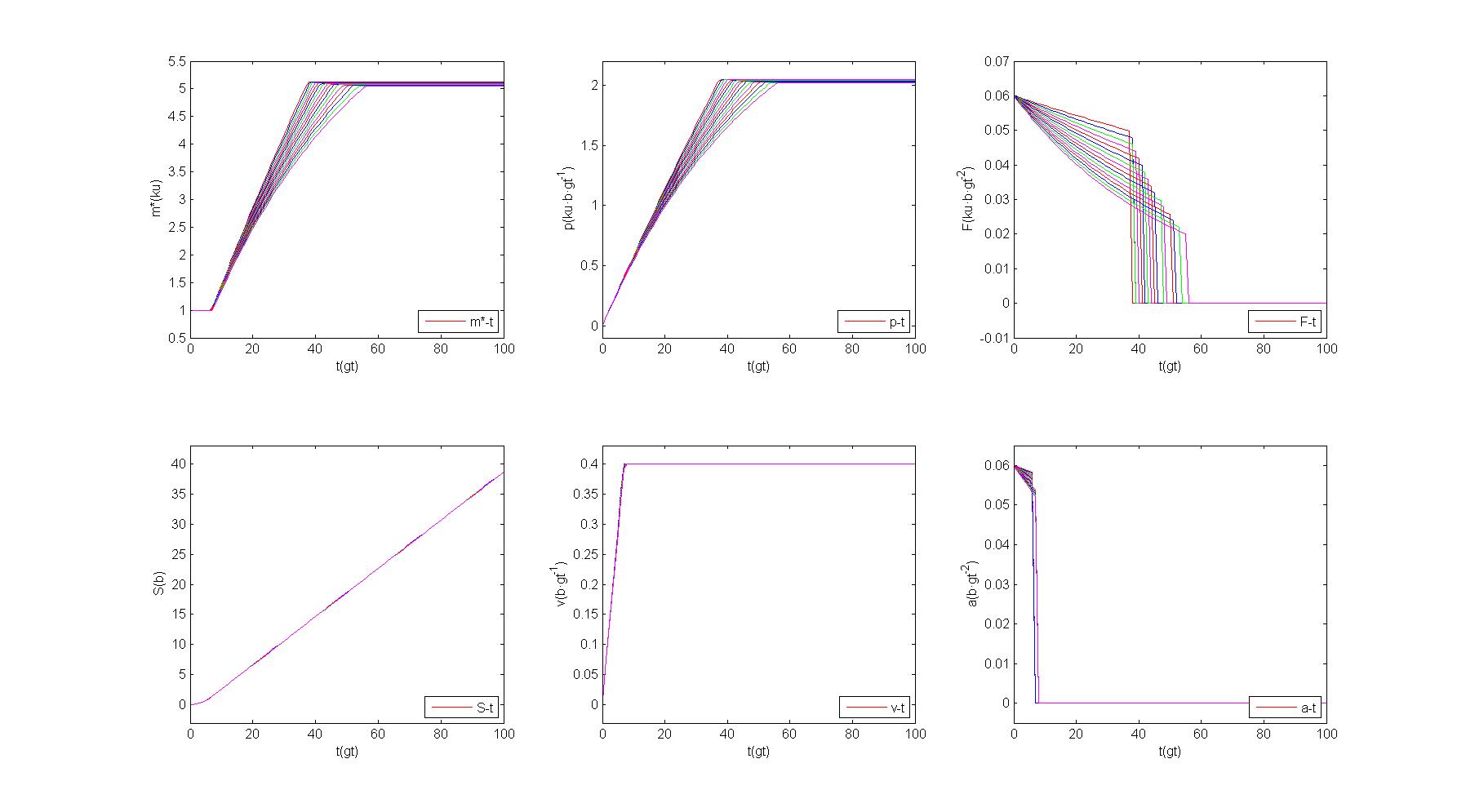
2.更多物理量之间的关系
除了[3]中所述的物理量,有必要引入更多的物理量,从而让我们更方便地描述整个体系。
1)饱和质量
饱和质量mmax 即矿车的饱和动量pmax 与饱和速度vmax 的比值,是仅与矿车种类和载物量h 有关的量。
2)有效质量
有效质量m* 即矿车动量p 和矿车速度v 的比值,其随耗时t 会产生变化。当动量和速度均未达到饱和时,有效质量m*=m ;当动量和速度均达到饱和时,有效质量m*=mmax 。
3)饱和常数
饱和常数B 即达到饱和速度的耗时tv 与达到饱和动量的耗时tp 的比值,是仅与矿车种类和载物量h 有关的量。

4)数学模型中的所有参数
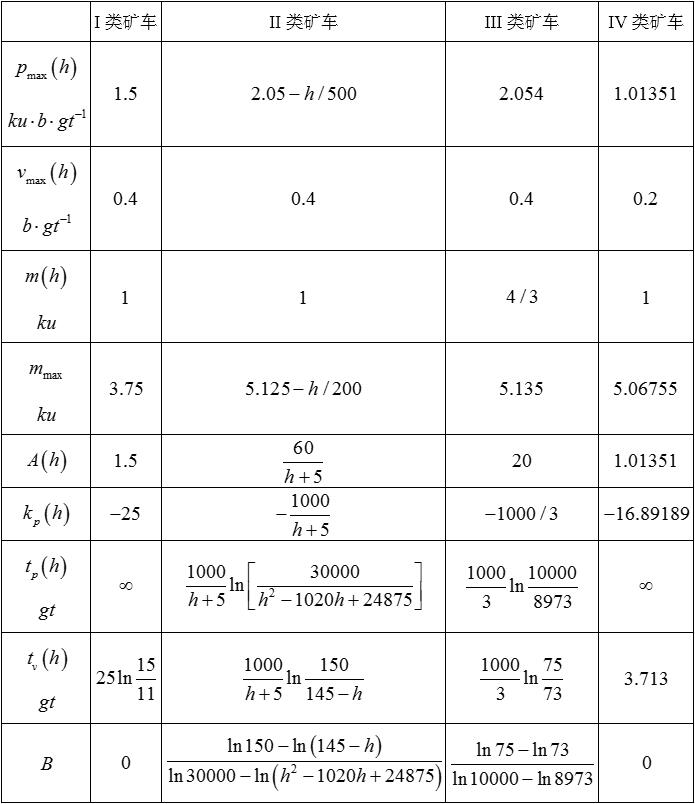
3.Matlab代码
1)定义Irail函数
定义Irail函数,给定矿车种类Kind、载物量h和耗时t,返回矿车的p、F、S、v、a。
function [OU] = Irail(Kind,h,t,na)
%设置初始参数
pmax=[1.5, 2.05-h./500, 2.054, 1.01351];
vmax=[0.4, 0.4, 0.4, 0.2];
m=[1, 1, 4/3, 1];
A=[1.5, 60./(h+5), 20, 1.01351];
kp=[-25, -1000./(h+5), -1000./3, -16.89189];
%计算其他参数
tp=kp(Kind).*log(1-pmax(Kind)./A(Kind));
tv=kp(Kind).*log(1-m(Kind).*vmax(Kind)./A(Kind));
mmax=pmax(Kind)./vmax(Kind);
B=tv./tp;
%计算p,F,S,v,a
p=min(A(Kind).*(1-exp(t./kp(Kind))),pmax(Kind));
F=-(1-sign(t-tp))./2.*A(Kind)./kp(Kind).* exp(t./kp(Kind));
Ss= A(Kind) ./m(Kind).*(tv+kp(Kind).* (1-exp(tv./kp(Kind))));
S= (1-sign(t-tv))./2.*A(Kind) ./m(Kind).*(t+kp(Kind).* (1-exp(t./kp(Kind))))+ (1+sign(t-tv))./2.*( Ss+(t-tv).*vmax(Kind));
v= min(A(Kind)./m(Kind).*(1-exp(t./kp(Kind))),vmax(Kind));
a=-(1-sign(t-tv))./2.*A(Kind) ./m(Kind)./kp(Kind).* exp(t./kp(Kind));
%函数输出
temp=[p,F,S,v,a,tp,tv,B,pmax(Kind),vmax(Kind),m(Kind),mmax,A(Kind),kp(Kind)];
switch na
case 'p'
OU=temp(1);
case 'F'
OU=temp(2);
case 'S'
OU=temp(3);
case 'v'
OU=temp(4);
case 'a'
OU=temp(5);
end
end
2)绘制不同矿车种类的运动学和动力学规律
clear
clc
tstart=0;
tend=100;
tstep=1;
Type=2;
h=0;
for Type=1:4
i=1;
for t=tstart:tstep:tend;
t2(i)=t;
M=Irail(Type,h,t,'p')./Irail(Type,h,t,'v');
M2(i)=M;
i=i+1;
end
subplot(2,3,1);
plot(t2,M2);
xlabel(' t(gt)')
ylabel(' m*(ku)')
legend('m*-t',4);
ylim([0.5 5.5]);
hold on;
end
na='p';
for Type=1:4
i=1;
for t=tstart:tstep:tend;
t2(i)=t;
M=Irail(Type,h,t,na);
M2(i)=M;
i=i+1;
end
subplot(2,3,2);
plot(t2,M2);
xlabel(' t(gt)')
ylabel(' p(ku·b·gt^-^1)')
legend('p-t',4);
ylim([-0.1 2.2]);
hold on;
end
na='F';
for Type=1:4
i=1;
for t=tstart:tstep:tend;
t2(i)=t;
M=Irail(Type,h,t,na);
M2(i)=M;
i=i+1;
end
subplot(2,3,3);
plot(t2,M2);
xlabel(' t(gt)')
ylabel(' F(ku·b·gt^-^2)')
legend('F-t',4);
ylim([-0.01 0.07]);
hold on;
end
na='S';
for Type=1:4
i=1;
for t=tstart:tstep:tend;
t2(i)=t;
M=Irail(Type,h,t,na);
M2(i)=M;
i=i+1;
end
subplot(2,3,4);
plot(t2,M2);
xlabel(' t(gt)')
ylabel(' S(b)')
legend('S-t',4);
ylim([-3 43]);
hold on;
end
na='v';
for Type=1:4
i=1;
for t=tstart:tstep:tend;
t2(i)=t;
M=Irail(Type,h,t,na);
M2(i)=M;
i=i+1;
end
subplot(2,3,5);
plot(t2,M2);
xlabel(' t(gt)')
ylabel(' v(b·gt^-^1)')
legend('v-t',4);
ylim([-0.03 0.43]);
hold on;
end
na='a';
for Type=1:4
i=1;
for t=tstart:tstep:tend;
t2(i)=t;
M=Irail(Type,h,t,na);
M2(i)=M;
i=i+1;
end
subplot(2,3,6);
plot(t2,M2);
xlabel(' t(gt)')
ylabel(' a(b·gt^-^2)')
legend('a-t',4);
ylim([-0.005 0.065]);
hold on;
end
3)绘制不同载物量的II类矿车的运动学和动力学规律
clear
clc
tstart=0;
tend=100;
tstep=1;
Type=2;
h=0;
for h=0:15
i=1;
for t=tstart:tstep:tend;
t2(i)=t;
M=Irail(Type,h,t,'p')./Irail(Type,h,t,'v');
M2(i)=M;
i=i+1;
end
subplot(2,3,1);
plot(t2,M2);
xlabel(' t(gt)')
ylabel(' m*(ku)')
legend('m*-t',4);
ylim([0.5 5.5]);
hold on;
end
na='p';
for h=0:15
i=1;
for t=tstart:tstep:tend;
t2(i)=t;
M=Irail(Type,h,t,na);
M2(i)=M;
i=i+1;
end
subplot(2,3,2);
plot(t2,M2);
xlabel(' t(gt)')
ylabel(' p(ku·b·gt^-^1)')
legend('p-t',4);
ylim([-0.1 2.2]);
hold on;
end
na='F';
for h=0:15
i=1;
for t=tstart:tstep:tend;
t2(i)=t;
M=Irail(Type,h,t,na);
M2(i)=M;
i=i+1;
end
subplot(2,3,3);
plot(t2,M2);
xlabel(' t(gt)')
ylabel(' F(ku·b·gt^-^2)')
legend('F-t',4);
ylim([-0.01 0.07]);
hold on;
end
na='S';
for h=0:15
i=1;
for t=tstart:tstep:tend;
t2(i)=t;
M=Irail(Type,h,t,na);
M2(i)=M;
i=i+1;
end
subplot(2,3,4);
plot(t2,M2);
xlabel(' t(gt)')
ylabel(' S(b)')
legend('S-t',4);
ylim([-3 43]);
hold on;
end
na='v';
for h=0:15
i=1;
for t=tstart:tstep:tend;
t2(i)=t;
M=Irail(Type,h,t,na);
M2(i)=M;
i=i+1;
end
subplot(2,3,5);
plot(t2,M2);
xlabel(' t(gt)')
ylabel(' v(b·gt^-^1)')
legend('v-t',4);
ylim([-0.03 0.43]);
hold on;
end
na='a';
for h=0:15
i=1;
for t=tstart:tstep:tend;
t2(i)=t;
M=Irail(Type,h,t,na);
M2(i)=M;
i=i+1;
end
subplot(2,3,6);
plot(t2,M2);
xlabel(' t(gt)')
ylabel(' a(b·gt^-^2)')
legend('a-t',4);
ylim([-0.005 0.065]);
hold on;
end
4.参考文献
[1] 《水平动力直轨(I类铁轨)对不同矿车加速作用的数学模型》
版权属于: Redstone Machinery Communication
原文地址: http://www.rmcteam.org/machinery-circiut/railway/model_rail_i_perfect.html
转载时必须以链接形式注明原始出处及本声明。