8-16 597 views
作者:nenn(百度id:正正正正正好)
注1:本文中提到的所有Minecraft版本均为1.12。
注2:相关数学推导需要高等数学知识(大学理工科专业一年级内容),涉及求导、微分和积分的计算。
1.理论推导
从[1]中我们已经清楚地认识到,数学模型可以加快铁路系统的研究效率。通过数学建模,我们已经可以通过计算获得I类和II类铁轨上所有种类矿车的运动细节。那么,是否有办法在已知I类铁轨的数量后,计算出矿车在II类铁轨上的最远滑行距离呢?肯定是有的。
如果仔细研究[1]和[2]就会发现,通过消去参变量t 后,可以获得任何两个物理量之间的关系。这样,我们就能获得矿车在I类铁轨上滑行的距离S 与离开I类铁轨时的动量p 以及驶入II类铁轨时的动量p0 与矿车可以滑行的最远距离Smax之间的关系。
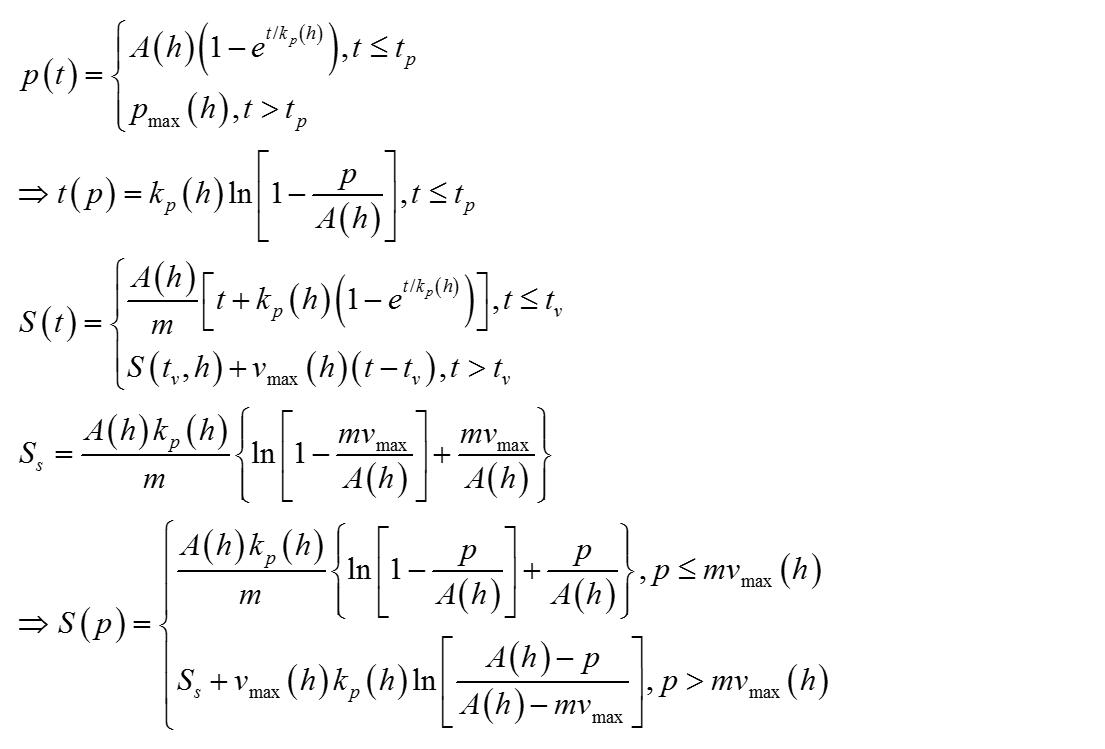
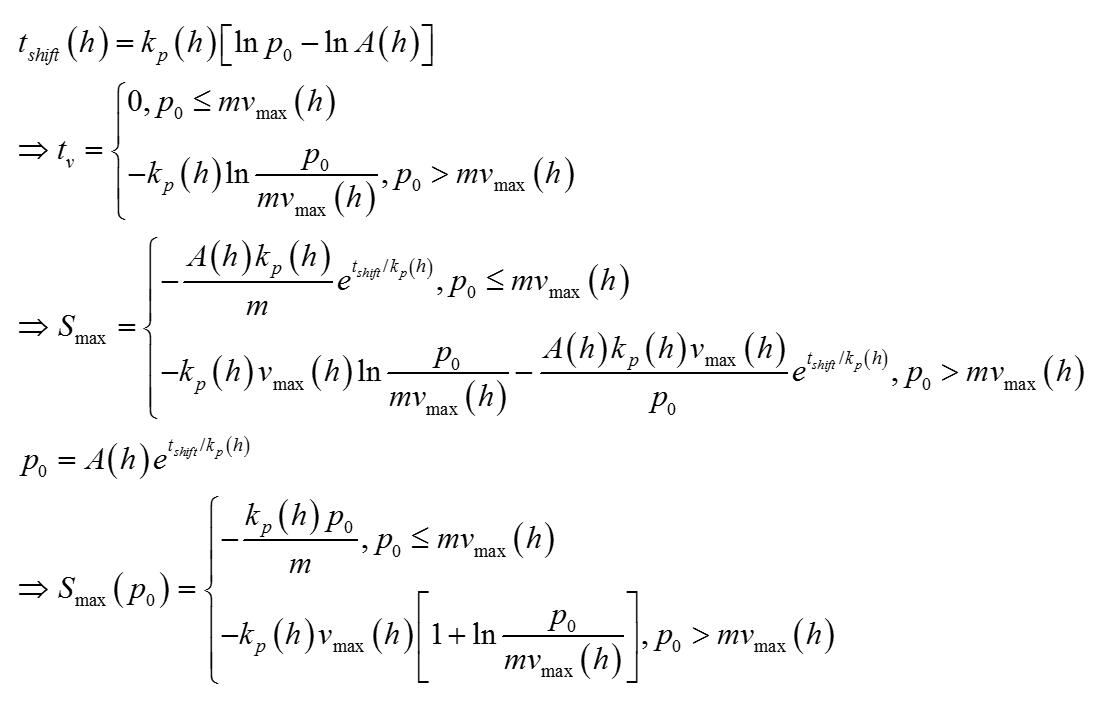
在I类铁轨和II类铁轨的交界处,矿车的动量是不会发生突变的。即存在关系p0=p 。如此可以获得S(Smax)的表达式。
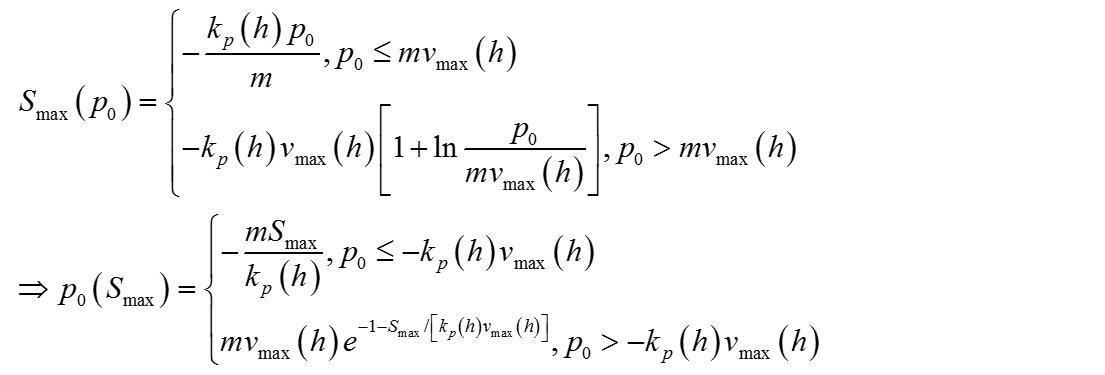

需要注意到的是,任何矿车经过2格或者更多的I类铁轨后,就已经达到了饱和速度。所以一般可以认为,S(Smax) 基本遵循下面的规律:
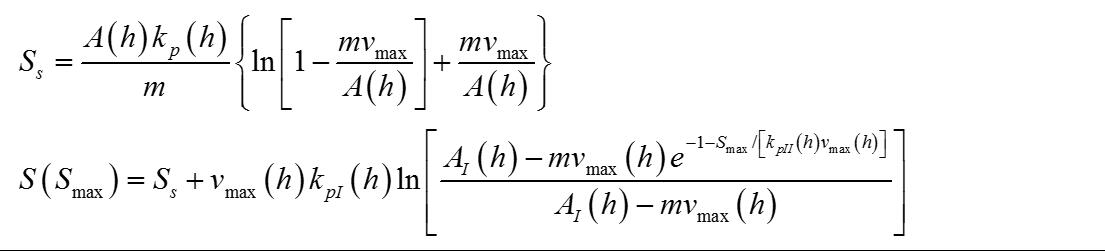
2.Matlab仿真
1)定义SSm函数
function [OU] = SSm(Kind,h,Smax)
Zpmax=[1.5, 2.05-h./500, 2.054, 1.01351];
pmax=Zpmax(Kind);
Zvmax=[0.4, 0.4, 0.4, 0.2];
vmax=Zvmax(Kind);
Zm=[1, 1, 4/3, 1];
m=Zm(Kind);
ZA1=[1.5, 60./(h+5), 20, 1.01351];
A1=ZA1(Kind);
Zkp1=[-25, -1000./(h+5), -1000./3, -16.89189];
kp1=Zkp1(Kind);
ZA2=[1.54245, 2, 2, 1.15682];
A2=ZA2(Kind);
Zkp2=[-25, -1000./(h+5), -1000./3, -16.89189];
kp2=Zkp2(Kind);
tp1=kp1.*log(1-pmax./A1);
tv1=kp1.*log(1-m.*vmax./A1);
Ss= A1./m.*(tv1+kp1.* (1-exp(tv1./kp1)));
TEMP1=m.*Smax./A1./kp2;
TEMP2=exp(-1-Smax./kp2./vmax);
TEMP3=-kp2.*pmax./m;
if Smax<=TEMP3
S=A1.*kp1./m.*(log(1+TEMP1)-TEMP1);
else
S=Ss+vmax.*kp1.*log((A1-m.*vmax.*TEMP2)./( A1-m.*vmax));
end
OU=S
end
2)绘制不同矿车种类的S-Smax关系
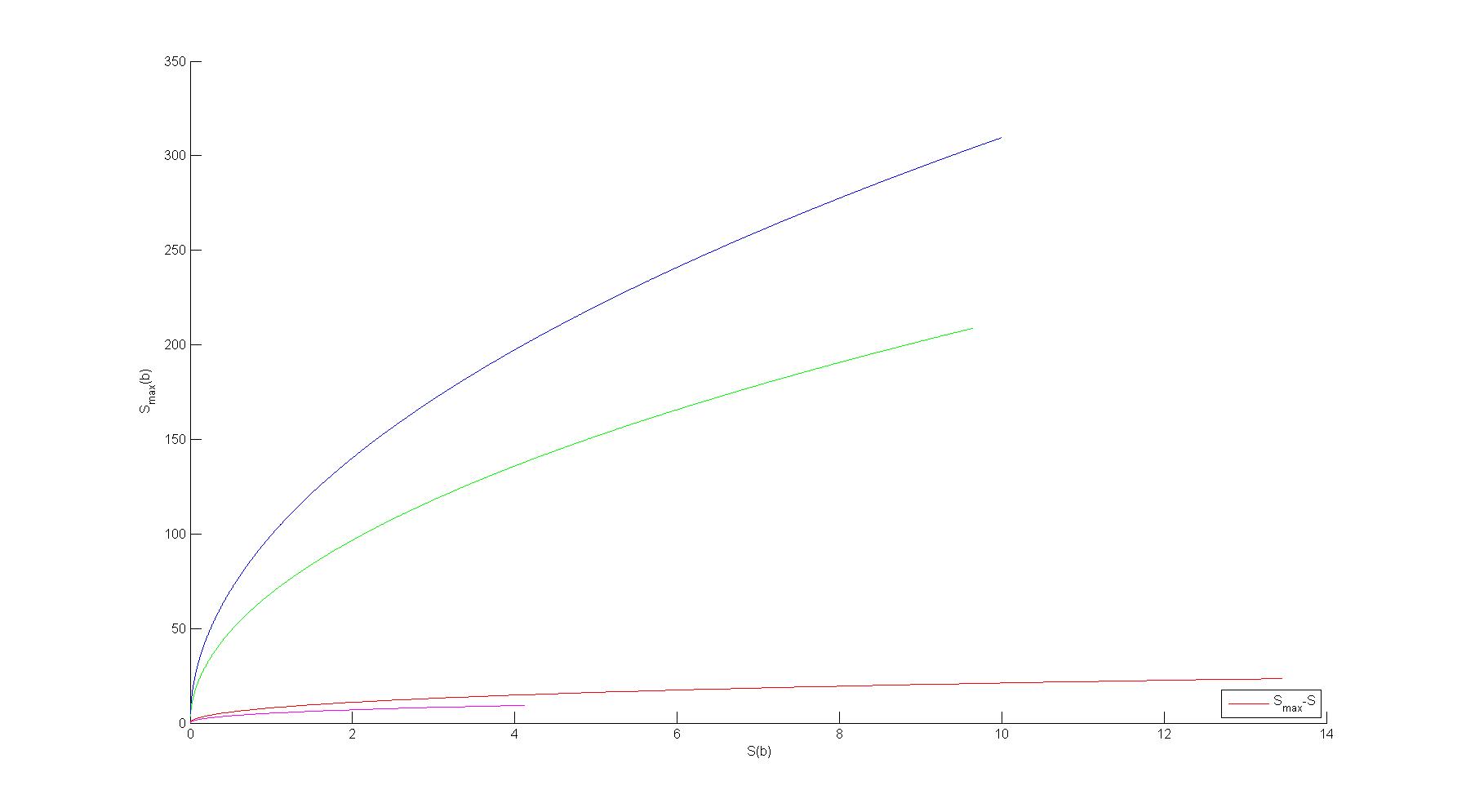
clear
clc
h=0;
Slim=[23.5,400./(h+5).*(1+log(5)),400./3.*(1+log(15./4)),9.3];
c=['r','g','b','m'];
for Kind=1:4;
x=0:0.1:Slim(Kind);
y=SSm(Kind,h,x);
hold on;
plot(y,x,c(Kind));
xlabel(' S(b)')
ylabel(' S_m_a_x(b)')
legend('S_m_a_x-S',4);
hold on;
%ylim([-0.07 0.01]);
end
3)绘制不同载物量的II类矿车的S-Smax关系
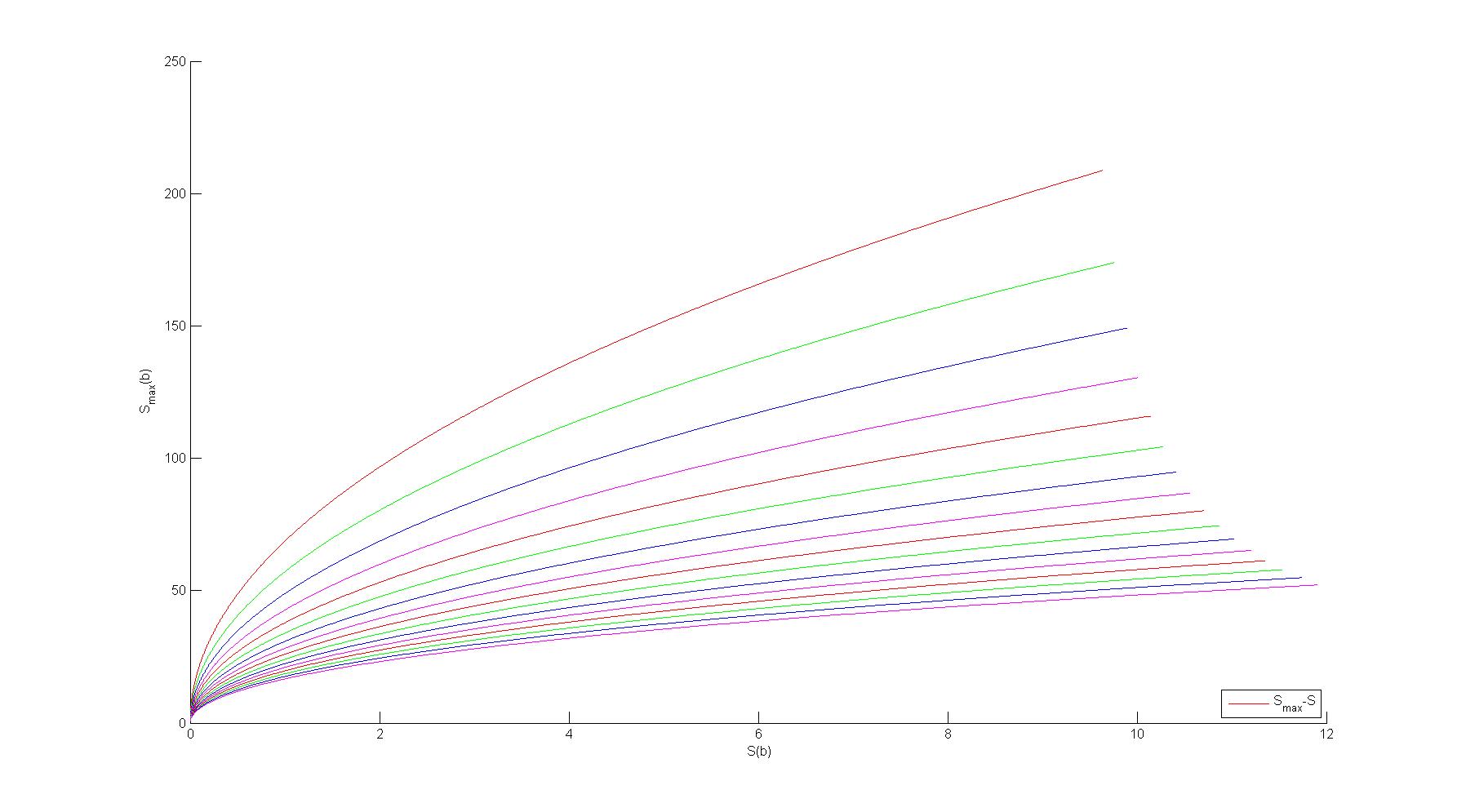
clear
clc
Kind=2;
c=['r','g','b','m','r','g','b','m','r','g','b','m','r','g','b','m'];
for h=0:15;
Slim=[23.5,400./(h+5).*(1+log(5)),400./3.*(1+log(15./4)),9.3];
x=0:0.1:Slim(Kind);
y=SSm(Kind,h,x);
hold on;
plot(y,x,c(h+1));
xlabel(' S(b)')
ylabel(' S_m_a_x(b)')
legend('S_m_a_x-S',4);
hold on;
%ylim([-0.07 0.01]);
end
3.仿真结果与实验数据的比较
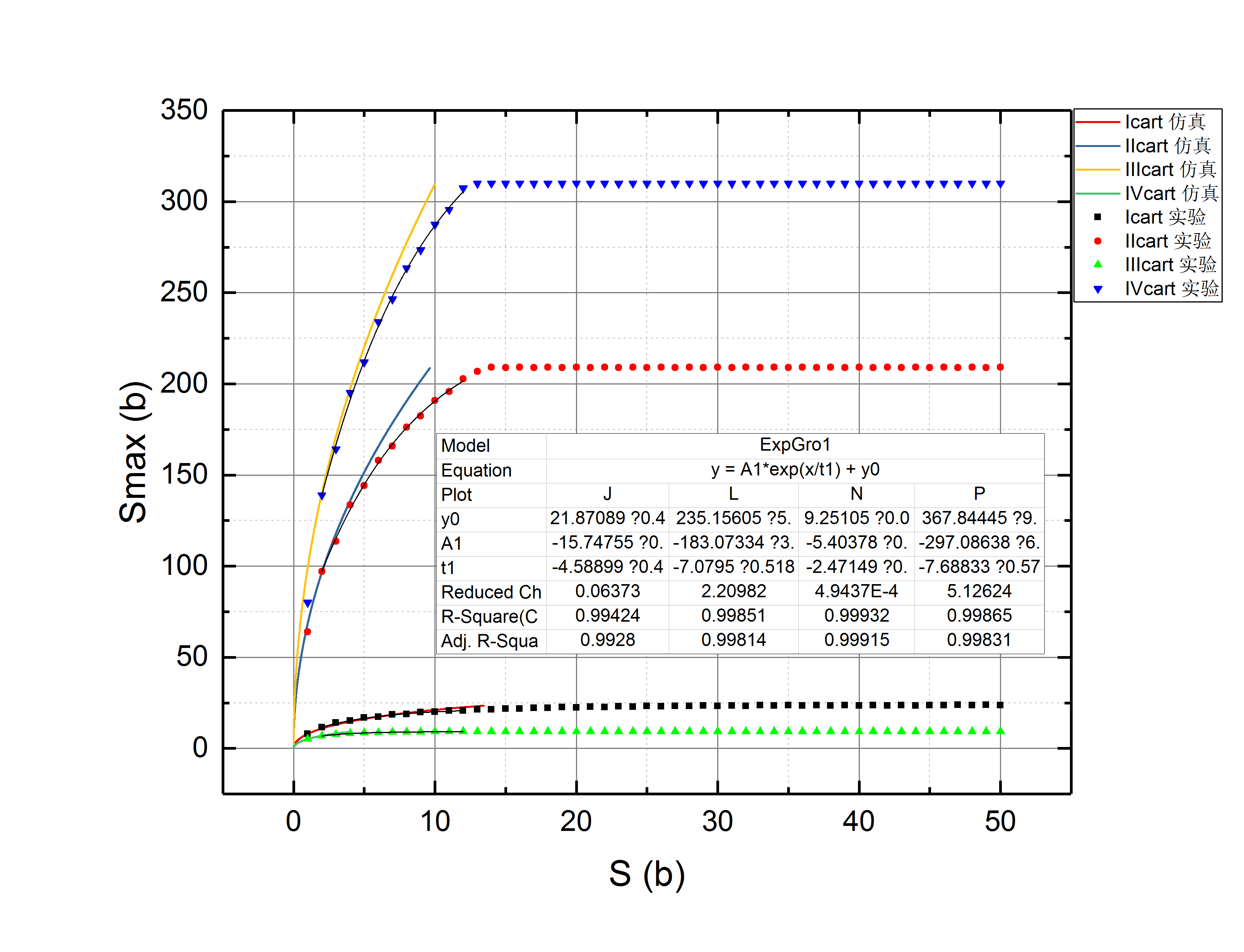
从实验结果和仿真结果的对比来看,仿真结果与实验结果的趋势相吻。通过数学模型推断出的1格I类铁轨情况的特殊性也获得了实验结果的支持。但较为可惜的是,随着I类铁轨的增加,模型的精准度开始下降,出现了较大的误差,此外,目前的模型也无法解释奇偶效应,即经过奇数格和偶数格I类铁轨作用后,在II类铁轨上滑行的最远距离会分布在拟合曲线两侧的现象。
4.参考文献
[1] 《水平阻尼直轨(II类铁轨)上矿车的运动学和动力学规律》
[2] 《水平动力直轨(I类铁轨)上矿车的运动学和动力学规律》
版权属于: Redstone Machinery Communication
原文地址: http://www.rmcteam.org/machinery-circiut/railway/s-smax.html
转载时必须以链接形式注明原始出处及本声明。