8-18 681 views
作者:nenn(百度id:正正正正正好)
注1:本文中提到的所有Minecraft版本均为1.12。
注2:本文在六氧化裙(百度id:l4m2)提出的原型程序的基础上完成,特此感谢。
1.数学模型的程序描述
基于[1]和[2]中的数学模型,尝试对这两者组合而成的轨道进行描述时,却遇到了困难[3]。仿真结果的误差会被放大,且模型无法解释奇偶效应。因此继续沿用这种模型对矿车进行描述不利于进一步深入了解矿车运动的细节。
我们发现一个很有趣的现象就是不同矿车的饱和动量[1]。比如II类和III类矿车的饱和动量pmax ,都非常接近2ku·b/gt,但却是精确的2.05-0.002*h和2.054。IV类矿车的饱和动量pmax 和kp 则看似是一个带有循环节的小数,这或许可以表达成某种分数的形式。此外,奇偶效应似乎暗示了铁轨能够分辨矿车滑行的距离。
我们注意到一个细节,就是饱和动量有时并不是整数,但可以通过一定的方法将饱和动量与某一个分数互相联系起来。比如:
I类矿车:1.5·(1+1/kp)+0.006=pmax
II类矿车:2·(1+1/kp)+0.006=pmax
III类矿车:2·(1+1/kp)+0.006=pmax
IV类矿车:75/74·(1+1/kp)+0.006=pmax
我们理解矿车的运动是根据游戏代码运行的结果来呈现的。可以作一个合理的假设,即游戏内存在这样一个函数,每一个游戏刻内,它会读取矿车的位置和动量,然后根据矿车所在的轨道,决定更新后的位置和动量。如果它获知矿车在更新后可能达到了饱和动量,则会强制限制矿车的动量和速度。这样一来我们就可以猜测,所谓的饱和动量只不过是程序进行了上述判断后又进行了一些操作,导致最后的动量保留了微小改变。
如果按照这个思路思考,可以猜测,每一个游戏刻内,这个函数做了下面的几件事情:
1)读取矿车的Motion和Position
2)根据Motion和矿车质量,计算矿车对应的速度。如果这个速度大于饱和速度,则将速度限制为饱和速度。然后确定更新后的Position。
3)检查Motion是否大于某个特定值。如果大于,则将其限制为这个特定值。
4)将Motion值乘以一个小于1的数以模拟阻尼作用。
5)如果矿车处于I类铁轨上,则Motion值再增加一定的量。如果处在II类铁轨上,则不做任何操作。
我们看到,加入矿车的Motion值达到了某个特定值后,那么在这样的过程中,Motion值被进行了一定的操作以后,会停留在饱和动量上。根据这种思路,很容易推测出,对于Motion进行的操作类似这样:
if Motion/m<vmax
Position=Position+Motion/m;
else
Position=Position+vmax;
end
if Motion>pmax
Motion=pmax;
end
Motion=Motion*C1;
if cart is on Irail
Motion=Motion+C2;
end
根据之前获得的数学模型[1]和[2],很容易写出这样的一个函数:
function [OU] = cart_brom(na,h,Kindc,Kindr)
Motion=na(1);
Pos=na(2);
qai=[1,0];
damp=[0.96,0.995-0.001*h,0.997,0.9408];
vmax=[0.4,0.4,0.4,0.2];
pmax=[1.5,2,2,75/74];
km=[1,1,0.75,1];
if km(Kindc)*Motion>vmax(Kindc)
Pos=Pos+vmax(Kindc);
else
Pos=Pos+km(Kindc)*Motion;
end
if Motion>pmax(Kindc)
Motion=pmax(Kindc);
end
Motion=Motion.*damp(Kindc);
Motion=Motion+0.06*qai(Kindr);
OU=[Motion,Pos];
end
实验上观察到的现象是,置于I类铁轨上的矿车,起步的Motion值变化为0.02。如果将这作为Motion值的初始值,则可以得到所有矿车在I类铁轨上的运动过程,我们可以获知每一时刻的Motion值和Position值。
我们假设I类铁轨从0往坐标负方向铺展,II类铁轨从0往坐标正方向铺展,假设矿车的初始Position分别为-49.5,-48.5,……,-0.5,那么可以绘制出矿车在上面运动的过程中,每一时刻的Position值和Motion值。
clear
clc
c=['r','b','g','m'];
h=0;
Kindc=2;
for lams=-49.5:-0.5
for Kindc=1:4
na=[0.02,lams];
tius=2000;
t=1:tius;
for i=1:tius
if na(2)<0
na=cart_brom(na,h,Kindc,1);
else
na=cart_brom(na,h,Kindc,2);
end
qiapos(i)=na(2);
qiamot(i)=na(1);
end
plot(t,qiapos,c(Kindc))
hold on;
end
end
xlabel('t(gt)');
ylabel('Position');
获得Position-t图像:
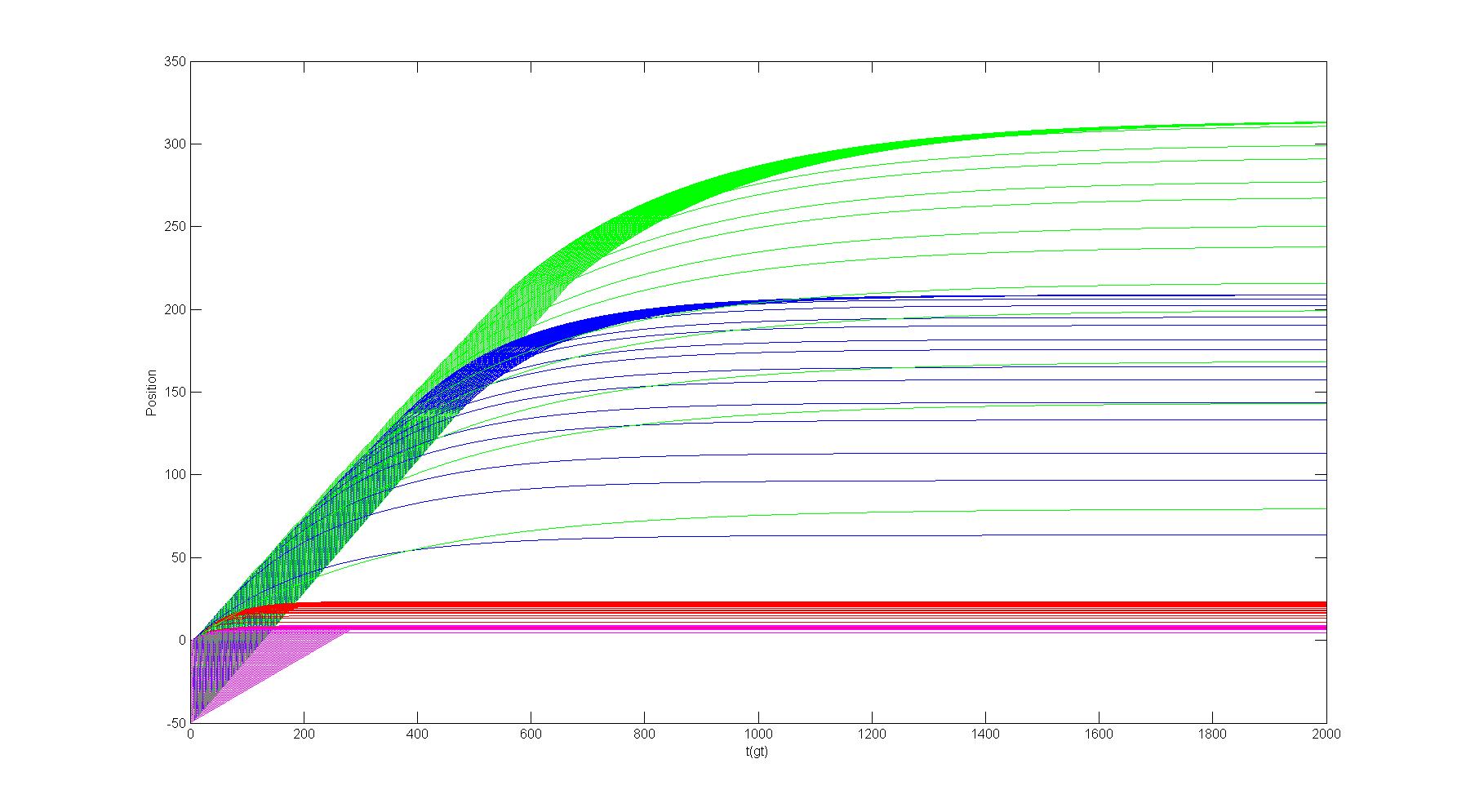
clear
clc
c=['r','b','g','m'];
h=0;
Kindc=2;
for lams=-49.5:-0.5
for Kindc=1:4
na=[0.02,lams];
tius=2000;
t=1:tius;
for i=1:tius
if na(2)<0
na=cart_brom(na,h,Kindc,1);
else
na=cart_brom(na,h,Kindc,2);
end
qiapos(i)=na(2);
qiamot(i)=na(1);
end
plot(t,qiamot,c(Kindc))
hold on;
end
end
xlabel('t(gt)');
ylabel('Motion');
获得Motion-t图像:
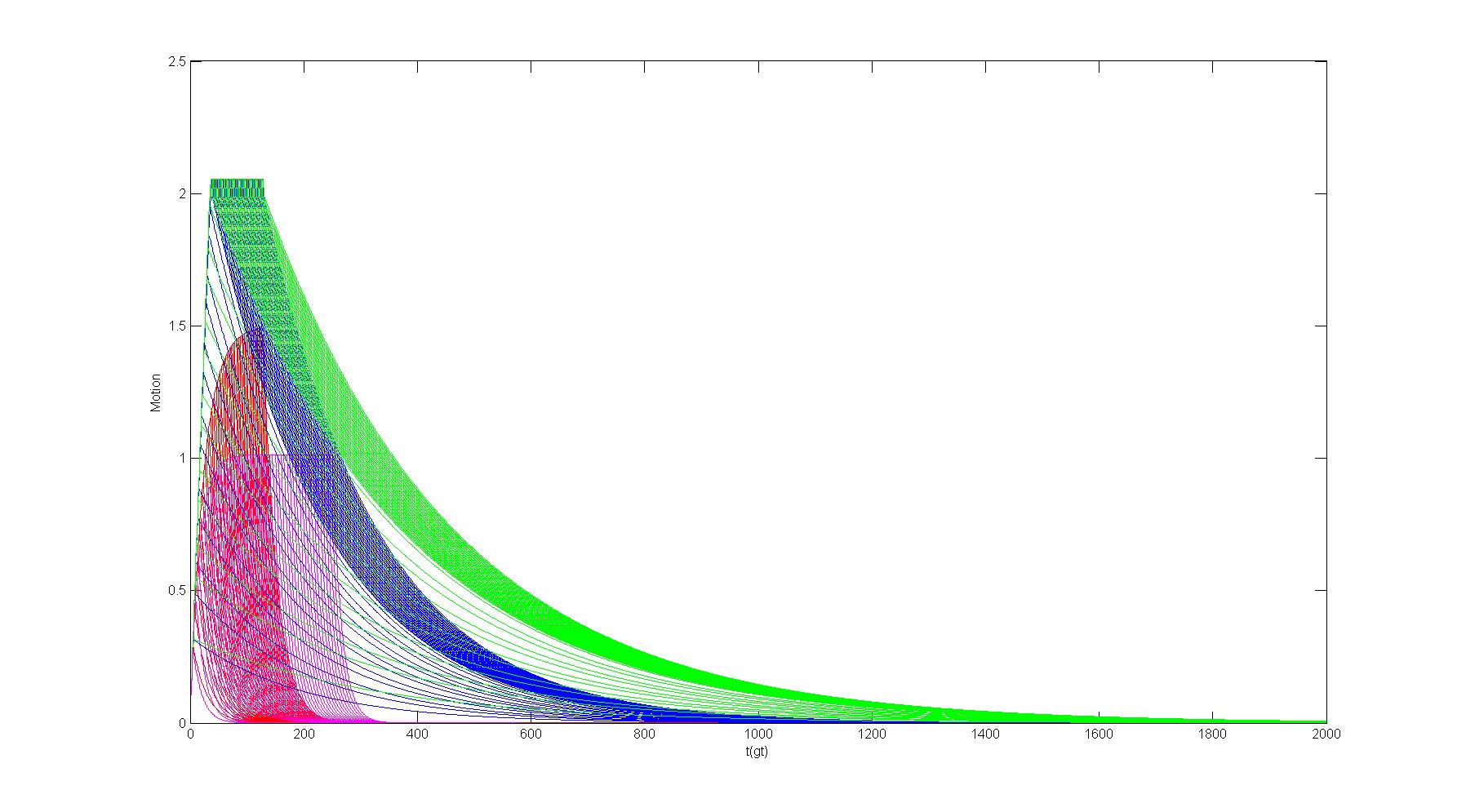
2.仿真结果与实验结果的对比
通过这样的程序,我们可以验证程序仿真的结果是否与实验结果相吻合。
1)饱和动量
I类矿车:1.5*0.96+0.06=1.5=pmax
II类矿车:2*(0.995-0.001*h)+0.06=2.05-0.002*h=pmax
III类矿车:2*0.997+0.06=2.054=pmax
IV类矿车:75/74*0.9408+0.06=75/74=pmax
仿真结果与实验相吻。
2)滑行最远距离
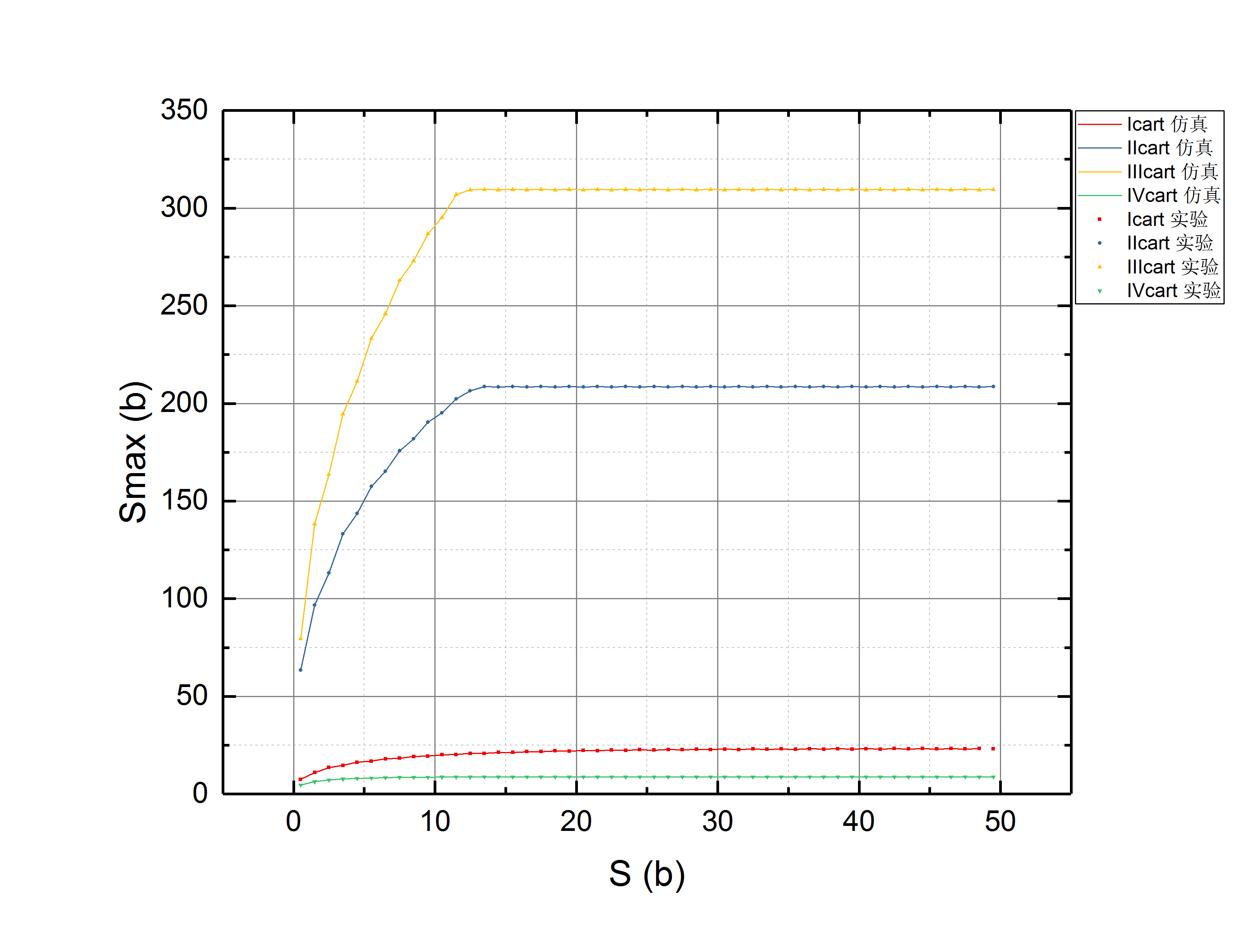
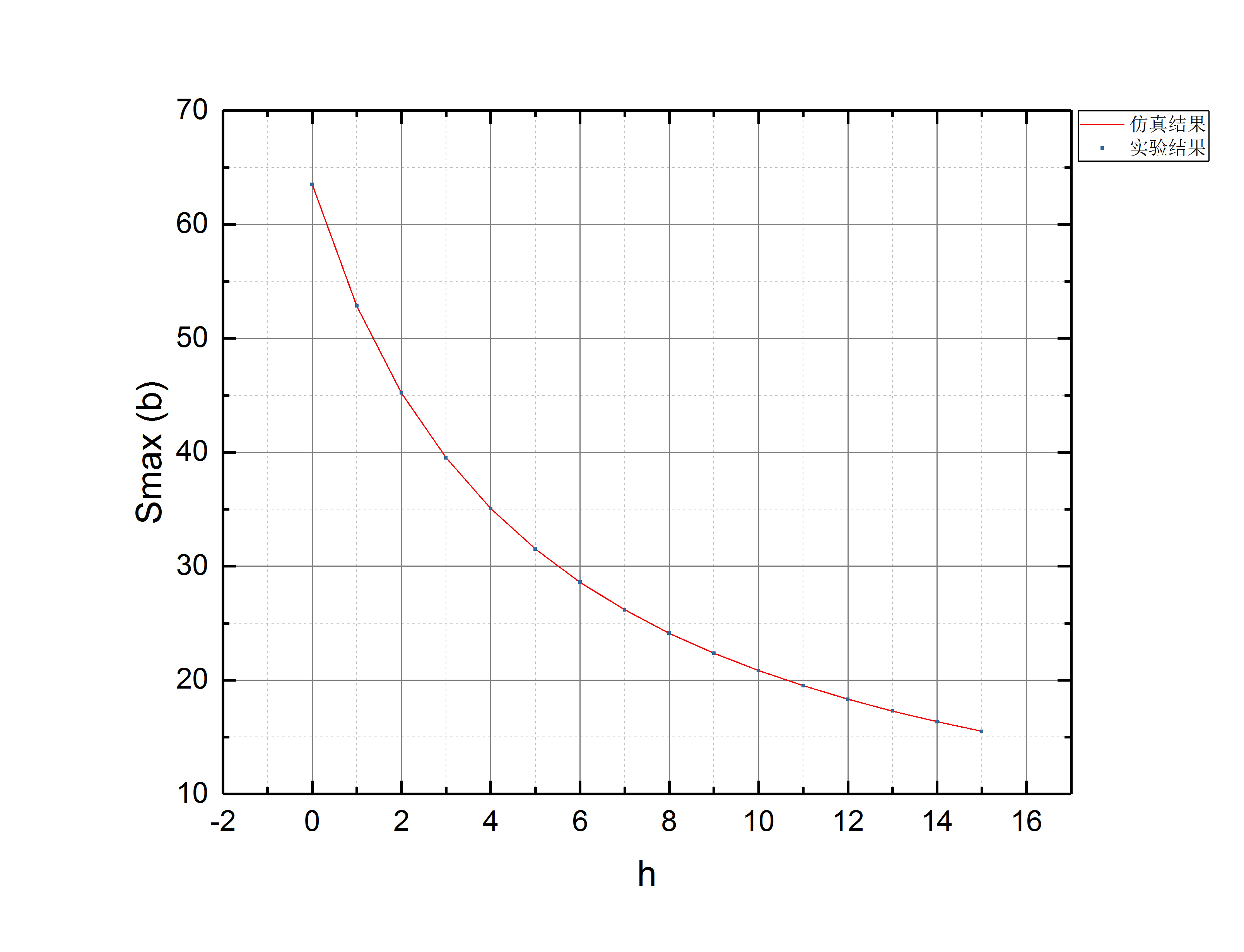
可见,仿真结果与实验结果吻合极佳,连奇偶效应也完美地重现了。
3.奇偶效应的来源
实验中发现存在这样的现象,即矿车达到饱和动量后,经过奇数格I类铁轨加速后,在II类铁轨上滑行的距离比经过偶数格I类铁轨加速后滑行的距离远0.2格。这种现象只会发生在I类、II类和III类矿车上,而IV类矿车没有类似的现象。通过上面归纳获得的矿车运动规律,可以发现奇偶效应的来源。
我们假设矿车分别经过2n格和2n+1格I类铁轨后进入II类铁轨滑行。一开始的加速过程没有区别,直至达到饱和动量。此时矿车一定已经以饱和速度前进。可以看到,如果以饱和速度每多通过一段铁轨,就需要1/vmax 的时间。对于I类、II类和III类矿车,vmax=0.4b/gt ,因此1/vmax=2.5gt 。但不是游戏刻整数倍的耗时是不存在的,因此实际的耗时是3游戏刻。这意味着,奇数格I类铁轨加速后,游戏认为矿车晚了0.5游戏刻进入II类铁轨。这0.5游戏刻等效于矿车移动了0.2格。这就是奇数格I类铁轨比偶数格II类铁轨能造成更远滑行距离的原因。反观IV类矿车,由于饱和速度为0.2格/游戏刻,因此不论奇数格还是偶数格I类铁轨,在I类铁轨上滑行的耗时都会是游戏刻的整数倍。因此IV类矿车不存在奇偶效应。
4.参考文献
[1] 《水平动力直轨(I类铁轨)上矿车的运动学和动力学规律》
[2] 《水平阻尼直轨(II类铁轨)上矿车的运动学和动力学规律》
[3] 《n格水平动力直轨加速矿车后可以在水平阻尼直轨上滑行多远?》
版权属于: Redstone Machinery Communication
原文地址: http://www.rmcteam.org/machinery-circiut/railway/i-ii-rail-brom.html
转载时必须以链接形式注明原始出处及本声明。