【游戏机制】自由落体的运动规律——理论部分

作者：nenn（百度id：正正正正正好）

注1：本文中提到的所有Minecraft版本均为1.8.8。

注2：禁庄转。

注3：高中以下学历可以适当跳过一些推导过程。相比推导过程，结论更加有用。

这里想说一些题外话。关于《【游戏机制】刷怪机制的可视化》一文，有部分玩家对相关的研究部分不以为然。这里我表示理解，因为即使把薛定谔方程放在他们眼前，他们也不会怎么重视它。然而他们并不知晓，没了薛定谔方程，他应该不可能看不到这个网页。这篇关于刷怪机制研究的文章，虽然研究的内容非常老套，但真正想展示的是一种全新的研究思路，内容的选择是为了检验和便于理解。CB技术玩家困于象牙塔，而生存技术玩家困于生存服务器，红石玩家困于被红石粉严重污染的MC世界（雾），互相鲜有交集。而这篇文章就是一声号角，它标志着CB技术与其他技术的交叉应用将极大促进技术本身的发展，CB技术的应用也将上升到一个新的层面。

---

自由落体的运动规律

我们知道，不同的实体在下落时具有不同的运动规律。关于这一点，Wiki实体 词条 提供了不同实体自由下落时的一些参数，包括加速度、阻尼、计算路程以及它们的顺序。其指出，由于阻尼的存在，最后所有的实体都会趋于匀速下落，而那个时候实体的下落速度即最终下落速度。

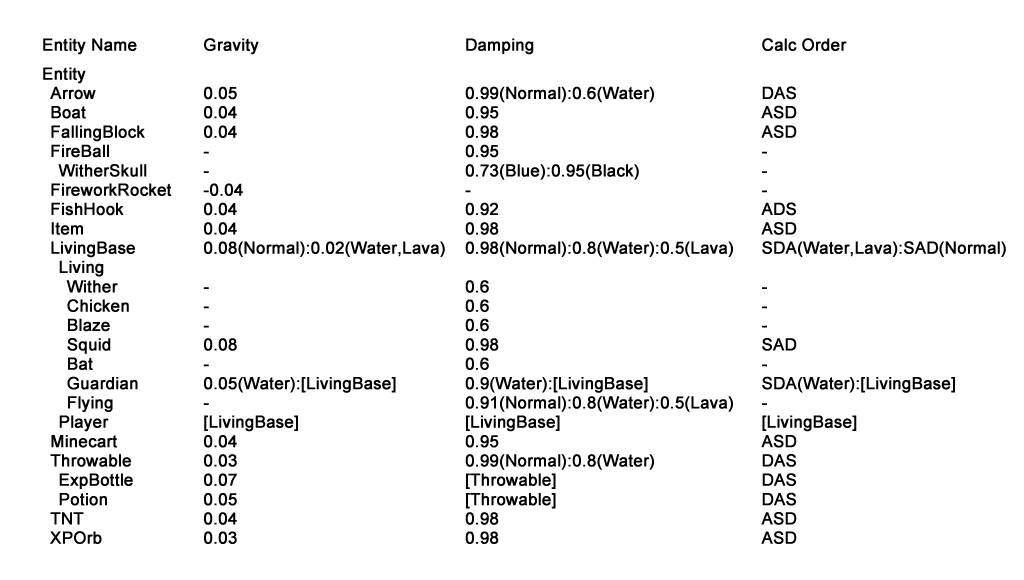
但是，Wiki中给出的参数并不够完整。所以咨询了来自TopologyCraft的gp(百度id：Gamepiaynmo)后，gp查阅了源代码给我们提供了这样一份数据。特别强调，下图中的数据来自gp，图片制作者也是gp。

Gravity表示的就是加速作用，单位是m/gametick^2；Damping表示的就是阻尼作用，单位是1/gametick。Calc Order表示的是加速作用和阻尼作用的先后顺序，A表示加速作用，D表示阻尼作用，S表示计算路程。

由于计算路程不影响速度，因此我们可以先来看看加速作用和阻尼作用的先后对下落速度造成的影响。

关于自由落体的速度

1）加速先于阻尼

对于这种情况，我们假设第t个游戏刻初实体的下落速度为v(t)【m/gametick】，加速度为a【m/gametick^2】，阻尼为f【1/gametick】。那么显然存在下面的关系：

v(1)=0······(1)

v(t+1)=[v(t)+a*1](1-f)=[v(t)+a](1-f)······(2)

可以发现，第t个和第t+1个游戏刻初实体的下落速度变化量为：

v(t+1)-v(t)=[v(t)+a](1-f)-v(t)=a-f[a+v(t)]······(3)

可以看到，当v(t)=a(1/f-1)时，v(t+1)-v(t)=0。此时实体的下落速度不再变化，稳定在v’。我们将v’称为最终下落速度。

v’=a(1/f-1)······(4)

虽然已知v(t)的递推公式，但是却还未得到v(t)的表达式。要得到v(t)的表达式并非很困难，虽然由递推公式可以看出v(t)并不满足等比或者等差这样的简单关系，但是其形式提醒我们可以构造一个等比数列。

v(t)的递推公式其经过等式变换以后，可以得到下面的形式：

[v(t+1)+L]=[v(t)+L](1-f)······(5)

那么v(t)+L就可以形成一个等比数列。基于这样的思维，我们很容易得到：

v(t+1)=[v(t)+L](1-f)-L=[v(t)+L-L/(1-f)](1-f)······(6)

经过对比，显然有下列关系成立：

L-L/(1-f)=a······(7)

所以我们就可以得到L的表达式：

L=-a(1/f-1)······(8)

我们惊讶地发现，L=-v’。那么现在，我们就成功构造了一个等比数列{v(t)-v’}：

[v(t+1)-v’]=[v(t)-v’](1-f)······(9)

由等比数列的通项公式易得：

v(t)-v’=[v(1)-v’](1-f)^(t-1)······(10)

v(t)=[v(1)-v’](1-f)^(t-1)+v’······(11)

代入初值v(1)=0，易得：

v(t)=v'[1-(1-f)^(t-1)]······(12)

于是我们就得到了v(t)的表达式。可以看到v(t)与最终下落速度v’的比值加一满足一个指数分布的关系。当然，说是指数关系，其实也是一个离散的满足指数分布的关系。也就是说这不是一个连续函数，这只是一个通项公式。这个规律和简单的高中物理可不太一样。这也就是为何许多欠考虑的研究会得到完全错误的分析结果。

根据上文的推导，经过t个游戏刻后，实体的下落速度达到了v(t)，我们假设其与v’的差值为daltav(t)=v’-v(t)，那么：

daltav(t)=v'(1-f)^(t-1)······(13)

我们注意到，Minecraft游戏中按下F2调出的窗口中，Y坐标的显示精度为e=10^(-5)m/gametick。这虽然并非游戏本身的计算精度，但是该精度下，我们已经无法从测量到的坐标上看出区别。因此，假设daltav(t’)=e，那么我们就可以得到实体自由落体达到最终下落速度所需要的时间t’。

e=v'(1-f)^(t’-1)······(14)

t’=ln(e/v’)/ln(1-f)+1······(15)

当然，特别强调，这一关系对于阻尼优先于加速的情况下也适用。

2）阻尼先于加速

使用类似的推导过程，我们完全可以得到阻尼先于加速作用下的规律：

v(1)=0······(1)

v(t+1)=v(t)(1-f)+a*1=v(t)(1-f)+a······(2)

v’=a/f······(3)

v(t)=v'[1-(1-f)^(t-1)]······(4)

t’=ln(e/v’)/ln(1-f)+1······(5)

3）小结

对于加速先于阻尼作用的情况下，最终速度为v’=a(1/f-1)；对于阻尼先于加速作用的情况下，最终速度为v’=a/f。

这两种情况下，自由落体后第t个游戏刻初实体的下落速度均为v(t)=v'[1-(1-f)^(t-1)]。其中v’为各自情况下得到的最终速度。同样，经过时间t’=ln(e/v’)/ln(1-f)+1个游戏刻后，我们可以认为实体已经达到了最终下落速度，因为此时速度的变化量已经小于坐标测速的精度，基于坐标测量速度已经无法识别速度的变化。

关于自由落体的下落高度

对于不同的实体，计算路程的过程并不总在特定的位置。因此我们不能再根据加速和阻尼的先后顺序来得到实体下落的高度。我们分别使用A、D、S表示加速作用、阻尼作用和计算下落高度以及它们的先后顺序。

1）ASD模式

我们先来研究第一种情况，即先计算加速，然后计算路程，最后计算阻尼，简称ASD。

ASD模式中，第t个游戏刻内实体的下落高度h'(t)为：

h'(t)=[v(t)+a]*1=a/f-v'(1-f)^(t-1)······(1)

因此自由落体t游戏刻后，实体下落的总高度h(t)为：

h(t)=[h'(1)+h'(2)+……+h'(t)]/(1-f)=[v(1)+v(2)+……+v(t)]+at=v'[t-S(t)]+at······(2)

其中：

S(t)=1+(1-f)+(1-f)^2+……+(1-f)^(t-1)······(3)

由等比数列前n项求和公式易知：

S(t)=[1-(1-f)^t]/f······(4)

故：

h(t)={at-v'[1-(1-f)^t]}/f······(5)

2）ADS和DAS模式

ADS模式则可以使用完全一样的思路推导。这里略去推导过程，直接给出结论。下同。

h'(t)=v'[1-(1-f)^t]······(1)

h(t)=v'{t-(1-f)[1-(1-f)^t]/f}······(2)

3）SAD和SDA模式

h'(t)=v'[1-(1-f)^(t-1)]······(1)

h(t)=v'{t-[1-(1-f)^t]/f}······(2)

4）DSA模式

幸运的是，虽然DSA模式的推导也稍微有些复杂，但游戏中并没有DSA模式。因此这里就不再进行推导。

总结

我们设置的参数、符号、他们的意义及单位罗列如下：

A：一个游戏刻内，对实体加速的计算

D：一个游戏刻内，对实体阻尼的计算

S：一个游戏刻内，对实体下落高度的计算

t：时间，单位为gametick，表示自由落体开始后的游戏刻数量

a：加速度，单位为m/gametick^2，表示的是每个游戏刻末与初的速度净增加量

f：阻尼，单位为1/gametick，表示的是每个游戏刻末与初的速度比值

v’：最终下落速度，单位为m/gametick，表示的是经过足够长的时间后，实体匀速下落时的速度

v(t)：下落速度，单位为m/gametick，表示自由落体开始后第t个游戏刻初的下落速度，且v(1)=0

h'(t)：单位时间的下落高度，单位为m，表示自由落体开始后第t个游戏刻内的下落高度

h(t)：下落总高度，单位为m，表示自由落体开始t个游戏刻后的下落高度

e：高度测量精度，其值为10^(-5)m，即0.00001m

t’：加速时间，单位为gametick，表示实体加速至最终下落速度所需要的时间。

---

特别感谢：

好时（百度id：Hershey4）为搭建官网做出的巨大贡献。

Dim White（百度id：滚大幕）提供的redstone_player皮肤及自由落体机制的讨论。

gp（百度id：Gamepiaynmo）提供的关于游戏代码中实体自由落体的机制和相关参数。

墨鱼服（OctopusCraft）全体。